Древовидные структуры данных являются одним из способов представления иерархической структуры и встречаются во многих предметных областях. Данная статья на простом примере рассматривает четыре наиболее популярных способа представления деревьев в реляционной базе данных.
Представление и хранение данных в виде дерева - часто встречающаяся задача в разработке программного обеспечения:
- XML/Markup синтаксические анализаторы, например Apache Xerces и Xalan XSLT, используют деревья;
- в основе формата PDF лежит дерево: корневой узел (root node) -> узел каталога (catalog node) -> узлы страниц (page nodes) -> узлы дочерних страниц (child page nodes). Обычно формат PDF в памяти представляют как сбалансированное дерево;
- многие научные и игровые программы применяют деревья решений, возможных вариантов, наборов поведения игроков. Например, шахматные программы строят огромные деревья возможных решений, библиотека визуализации Flare (http://flare.prefuse.org/) широко использует остовные деревья, с помощью деревьев решений брокеры определяют участвовать ли в торге.
Древовидные структуры данных являются одним из способов представления иерархической структуры и встречаются во многих предметных областях:
- двоичное дерево в информатике,
- филогенетическое дерево в биологии,
- финансовая пирамида в бизнесе,
- структура декомпозиции работ в управлении проектами;
- с помощью деревьев моделируют многоуровневые связи вида “главный - подчиненный”, “предок - потомок”, “целое - часть”, “общее - частное”.
Рассмотрим четыре наиболее популярных способа хранения деревьев в реляционной базе данных. В качестве примера возьмем каталог строительных материалов (рис. 1) и СУБД Postgres 9.6.
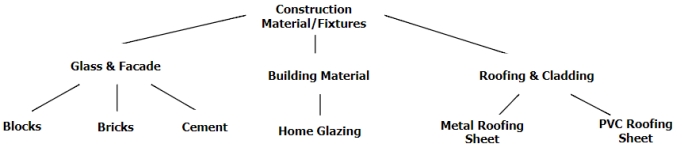
Рис 1. Каталог строительных материалов.
В теории графов деревом называется связный граф без циклов, в то время как лесом называется произвольный граф (возможно, несвязный) без циклов. Описываемые в данной статье методы могут без ограничения общности применяться для хранения как деревьев, так и лесов.
1. Список смежности (Adjacency List)
В теории графов списки смежности - один из способов представления графа, в котором для каждой вершины хранится список смежных с ней вершин. В случае дерева, если рассматривать все ребра как направленные от дочерних вершин к родительским, такие списки вырождаются в единственное значение, которое можно хранить вместе с самой вершиной. Этот способ хранения является самым часто встречающимся и интуитивно понятным: таблица ссылается сама на себя (рис. 2). Корневые узлы записываются с пустой ссылкой на предка (NULL).
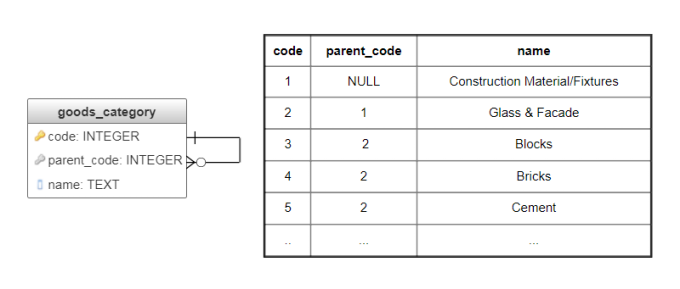
Рис. 2. Использование списка смежности
В этом способе для выполнения наиболее популярных выборок данных требуется поддержка рекурсивных запросов. PostgreSQL поддерживает такой вид запросов, в случае, если СУБД их не поддерживает, то выборки придется строить с помощью временных таблиц и хранимых процедур. Рассмотрим примеры запросов.
Выборка поддерева по заданному узлу:
WITH RECURSIVE sub_category(code, name, parent_code, level) AS (
SELECT code, name, parent_code, 1 FROM goods_category WHERE code=1 /* код заданного узла поддерева */
UNION ALL
SELECT c.code, c.name, c.parent_code, level+1
FROM goods_category c, sub_category sc
WHERE c.parent_code = sc.code
)
SELECT code, name, parent_code, level FROM sub_category;
Путь к узлу от корня:
WITH RECURSIVE sub_category(code, name, parent_code, level) AS (
SELECT code, name, parent_code, 1 FROM goods_category WHERE code=5 /* код узла */
UNION ALL
SELECT c.code, c.name, c.parent_code, level+1
FROM goods_category c, sub_category sc
WHERE c.code = sc.parent_code
)
SELECT code, name, parent_code, (SELECT max(level) FROM sub_category) - level AS distance FROM sub_category;
Проверка, входит ли узел дерева Cement (code=5) в Construction Material/Fixtures(code=1):
WITH RECURSIVE sub_category(code, name, parent_code, level) AS (
SELECT code, name, parent_code, 1 FROM goods_category WHERE code=5 /* код проверяемого элемента */
UNION ALL
SELECT c.code, c.name, c.parent_code, level+1
FROM goods_category c, sub_category sc
WHERE c.code = sc.parent_code
)
SELECT CASE WHEN exists(SELECT 1 FROM sub_category WHERE code=2 /*код корня поддерева, куда проверяется вхождение*/)
THEN 'true'
ELSE 'false'
END
Преимуществами этого метода являются:
- интуитивное представление данных (пары значений code, parent_code однозначно соответствуют ребрам дерева);
- при использовании списка смежности нет избыточности хранения, не требуется дополнительная поддержка целостности, кроме ссылочной (и, при необходимости, для предотвращения возникновения циклов);
- уровень вложенности дерева не ограничен;
- быстрые и простые операции вставки, перемещения и удаления узлов дерева, так как они не требуют изменений других узлов дерева.
К недостаткам можно отнести:
- необходимость использовать рекурсию для выборки всех потомков или предков узла, определения его уровня и количества потомков; данный способ хранения требует поддержки специфических функций СУБД и не может быть реализован эффективно в том случае, если СУБД такие функции не поддерживает. В случаях, когда использование рекурсии является невозможным или непроизводительным, часть преимуществ списка смежности может быть достигнута при помощи одноуровневой таблицы (flat table).
2. Подмножества (Subsets)
Также closure table (таблица связей) или bridge table (соединительная таблица).
В этом способе хранения дерево представляется в виде вложенных подмножеств, корневой узел содержит в себе все подмножества первого уровня, которые в свою очередь включают подмножества второго уровня, и так далее (рис. 3).
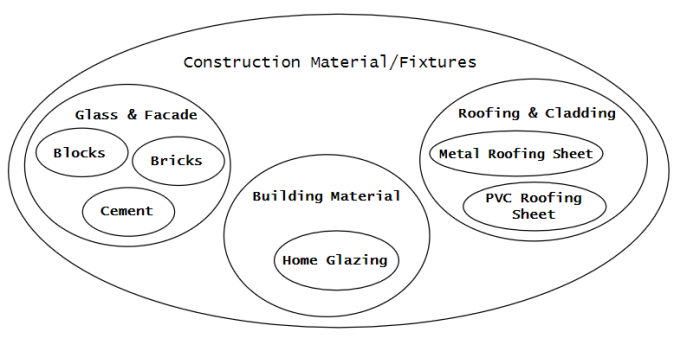
Рис 3. Представление дерева в виде вложенных подмножеств
Для хранения дерева таким способом понадобятся две таблицы: в одну таблицу записываются все подмножества (таблица goods_category, рис. 4), во вторую - список вхождений каждого подмножества в другие, а также их уровни (таблица subset, рис. 4).
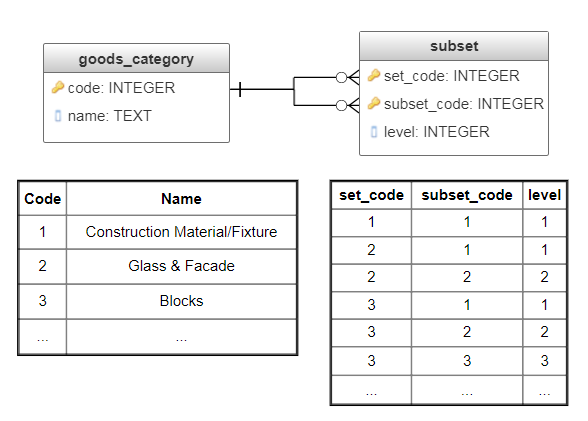
Рис. 4. Использование подмножеств
Таким образом, для каждого нового узла в таблицу subset необходимо добавить количество записей, равное уровню вложенности этого узла. Нетрудно заметить, что количество записей растет в арифметической прогрессии, но и типовые запросы становятся короче и работают быстрее, чем в предыдущем способе.
Выборка поддерева по заданному узлу:
SELECT name, set_code, subset_code, level FROM subset s
LEFT JOIN goods_category c ON c.code = s.set_code
WHERE subset_code = 1 /* корень поддерева */
ORDER BY level;
Путь к узлу от корня
SELECT name, set_code, subset_code, level FROM subset s
LEFT JOIN goods_category c ON c.code = s.subset_code
WHERE set_code = 3 /* узел */
ORDER BY level;
Проверка, входит ли Blocks (code=3) в Construction Material/Fixtures(code=1):
SELECT CASE
WHEN exists(SELECT 1 FROM subset
WHERE set_code = 3 AND subset_code = 1)
THEN 'true'
ELSE 'false'
END
При перемещении или вставке узла целостность данных сохраняется за счет триггеров, которые перезаписывают связанные с изменяемым узлом записи.
Главное достоинство метода подмножеств - быстрые, простые, не рекурсивные операции с деревом: выборка поддерева, всех предков узла, определение количества потомков узла и его уровня.
К недостаткам относятся:
- относительно неинтуитивное представление данных (восприятие усложняется из-за наличия избыточных связей между непрямыми потомками),
- избыточность хранения,
- использование триггеров для поддержки целостности данных;
- операции перемещения и вставки узлов в методе подмножеств сложнее, чем при использовании таблицы смежности. Для вставки нового узла придется добавить новые записи для всех его дочерних узлов, а при перемещении узла придется обновить записи у его предков и потомков.
3. Вложенные множества (Nested sets)
Идея этого метода заключается в хранении маршрута обхода дерева в префиксном порядке. В этом случае сначала посещается корень дерева, затем узлы левого поддерева в префиксном порядке, после - узлы правого поддерева также в префиксном порядке. Порядок обхода хранится в двух дополнительных полях left_key и right_key. В поле left_key записывается порядковый номер при входе в поддерево, а в right_key порядковый номер при выходе из поддерева (рис 5). Таким образом, номера потомков всегда располагаются в интервале между соответствующими номерами предка, независимо от их уровня относительно друг друга. Пользуясь этим свойством при составлении типовых запросов к дереву, можно легко обойтись без рекурсии.
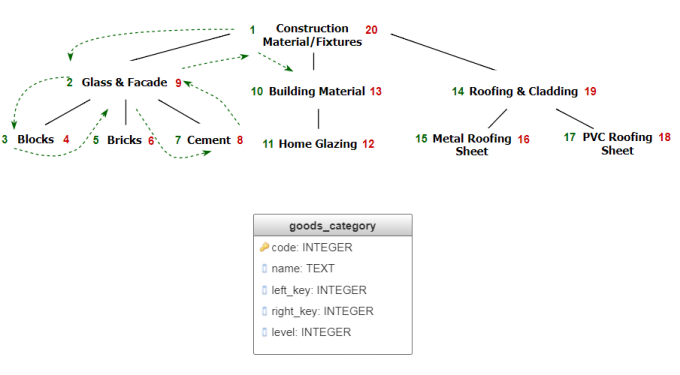
Рис. 5 Использование вложенных множеств
Выборка поддерева по заданному узлу:
WITH root AS (SELECT left_key, right_key FROM goods_category WHERE code=2 /*код узла*/)
SELECT * FROM goods_category
WHERE left_key >= (SELECT left_key FROM root)
AND right_key <= (SELECT right_key FROM root)
ORDER BY level;
Путь к узлу от корня:
WITH node AS (SELECT left_key, right_key FROM goods_category WHERE code=8 /*код узла*/)
SELECT * FROM goods_category
WHERE left_key <= (SELECT left_key FROM node)
AND right_key >= (SELECT right_key FROM node)
ORDER BY level;
Проверка, входит ли Blocks (code=3) в Construction Material/Fixtures(code=1):
SELECT CASE
WHEN exists(SELECT 1 from goods_category AS gc1, goods_category gc2
WHERE gc1.code = 1
AND gc2.code = 3
AND gc1.left_key <= gc2.left_key
AND gc1.right_key >= gc2.right_key)
THEN 'true'
ELSE 'false'
END
Положительными сторонами метода вложенных множеств можно назвать быстрые и простые операции выборки всех потомков, предков узла, их количества и уровня без использования рекурсии.
Основная сложность этого способа - необходимость переопределения порядка обхода при добавлении нового или перемещении существующего узла. Так, если добавить новый элемент в самый нижний уровень, то придется обновить поля left_key и right_key у всех узлов, которые находится “правее” и ”выше”, что, фактически, означает пересчет всего маршрута по дереву. Можно сократить количество обновлений маршрута обхода, если нумеровать left_key и right_key с некоторым интервалом, например, вместо “1” и “20” “10 000” и “200 000” соответственно. Это позволит вставить новый узел без полной перенумерации всех последующих. Аналогичным образом можно использовать в качестве left_key и right_key дробные числа.
4. Материализованные пути (Materialized paths)
Также lineage column (столбец преемственности)
Суть метода состоит в том, чтобы хранить полный путь от вершины до узла в явном виде в качестве первичного ключа (рис 6). Материализованные пути являются очень наглядным способом кодирования элементов дерева: каждый узел имеет интуитивно понятное значение, код узла и его части несут смысловую нагрузку. Это свойство является важным для классификаций, предназначенных для широкого пользования, таких как, справочник медицинских диагнозов, универсальная десятичная классификация (УДК), используемая в научных статьях, ее зарубежная коллега PACS (Physics and Astronomy Classification Scheme). Запросы при использовании этого метода выглядят лаконичными, но не всегда эффективны, так как часто используют поиск по подстроке.
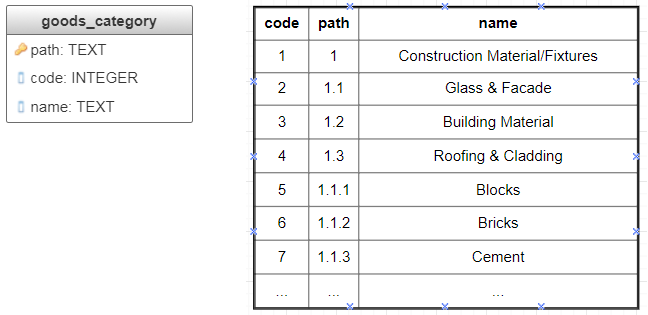
Рис. 6 Использование материализованных путей
Выборка поддерева по заданному узлу:
SELECT * FROM goods_category WHERE path LIKE '1.1%' ORDER BY path
Путь к узлу от корня:
SELECT * FROM goods_category WHERE '1.1.3' LIKE path||'%' ORDER BY path
Проверка, входит ли Cement в Construction Material/Fixtures:
SELECT CASE
WHEN exists(SELECT 1 FROM goods_category AS gc1, goods_category AS gc2
WHERE gc1.name = 'Construction Material/Fixtures'
AND gc2.name = 'Cement'
AND gc2.path LIKE gc1.path||'%')
THEN 'true'
ELSE 'false'
END
В случае, если заранее известно максимальное количество уровней и максимальное число потомков на каждом уровне, можно обойтись без разделителей и использовать числовые коды с фиксированной разбивкой на группы разрядов. Пустые разряды заполняются нулями. Также возможно использование отдельных столбцов для каждого уровня иерархии (multiple lineage columns): при таком подходе пропадает необходимость использовать поиск по подстроке. Подобная схема применяется во многих классификациях, например, ОКАТО, NAICS.
К преимуществам метода материализованных путей можно отнести интуитивность представления данных и простоту типовых запросов.
Недостатками метода являются сложные вставка нового узла дерева перемещение и удаление узла, избыточность хранения, сложность реализации поддержки целостности данных, неэффективные запросы, так как поиск выполняется по подстроке. Если материальные пути не используют разделители, а только числовые коды, то еще одним недостатком будет ограниченность количества уровней дерева.
4.1. Модуль ltree в PostreSQL
В PostgreSQL есть специализированный модуль для работы с деревьями ltree, который позволяет использовать метод материализованных путей более эффективно и удобно. Этот модуль реализует тип данных ltree для представления меток данных label, хранящихся в иерархической древовидной структуре, и средства для поиска по дереву. Разрешенными символами для меток данных являются буквы, цифры и знак подчеркивания, максимальная длина одной метки должна быть меньше 256 байт (L1, 42, building_materials). Путь от корня до какой-либо метки хранится в виде последовательности меток, разделенных точкой (L1.L2.L3), максимальный путь в дереве должен быть меньше 65 Kb, рекомендованный размер максимального пути ~ 2 Kb. В документации утверждается, что на самом деле, это несущественное ограничение, и в качестве примера приводится максимальная длина DMOZ каталога (http://dmoztools.net/) - 240 байт. Для поиска можно использовать шаблоны двух типов: lquery (регулярное выражение для сопоставления значений ltree) и ltxtquery (полнотекстовый шаблон поиска по значениям ltree). Ключевое различие между lquery и ltxtquery заключается в том, что ltxtquery ищет слова без учета их позиции в пути метки.
Рассмотрим запросы к нашему дереву с ltree:
Установим плагин, создадим таблицу и заполним ее данными:
CREATE EXTENSION "ltree";
CREATE TABLE goods_category_ltree (path ltree, name text);
INSERT INTO goods_category_ltree (path, name) VALUES
('construction_materials', 'Construction Material/Fixtures'),
('construction_materials.glass', 'Glass & Facade'),
('construction_materials.building_materials', 'Building Material'),
('construction_materials.roofing', 'Roofing & Cladding'),
('construction_materials.glass.blocks', 'Blocks'),
('construction_materials.glass.bricks', 'Bricks'),
('construction_materials.glass.cement', 'Cement'),
('construction_materials.building_materials.home_glazing', 'Home Glazing'),
('construction_materials.roofing.metal_sheet', 'Metal Roofing Sheet'),
('construction_materials.roofing.pvc_sheet', 'PVC Roofing Sheet');
Выборка поддерева по заданному узлу:
SELECT * FROM goods_category_ltree WHERE path @> (SELECT path FROM goods_category_ltree WHERE name = 'Blocks');
или
SELECT path, name FROM goods_category_ltree WHERE path ~ 'construction_materials.glass.*';
Путь к узлу от корня:
SELECT * FROM goods_category_ltree WHERE path <@ (SELECT path FROM goods_category_ltree WHERE name = 'Construction Material/Fixtures');
Проверка, входит ли Cement в Construction Material/Fixtures:
SELECT CASE WHEN exists(SELECT 1 FROM goods_category_ltree
WHERE (
SELECT path FROM goods_category_ltree WHERE name = 'Construction material/ Fixtures'
) @> (SELECT path FROM goods_category_ltree WHERE name = 'Cement'))
THEN 'true'
ELSE 'false'
END
Определить количество меток в пути (уровень)
SELECT path, nlevel(path) FROM goods_category_ltree WHERE name ='Blocks';
Заключение
Мы рассмотрели четыре популярных способа хранения древовидной структуры в реляционной базе данных. У каждого способа есть как свои достоинства, так и недостатки.
Из четырех методов только у списка смежности нет избыточности, нет необходимости в дополнительной поддержке целостности (кроме ссылочной); вставка и перемещение узлов дерева не затрагивают другие записи в таблице. Однако большинство типовых запросов для списка смежности используют рекурсию.
Для всех остальных рассмотренных способов рекурсия в запросах не требуется, но вставка и перемещение узлов не могут быть выполнены без обновления других, связанных с ними, узлов. Для способов хранения с помощью материализованных путей и вложенных множеств можно применить оптимизацию, хотя она и не убирает всех ограничений этих методов.
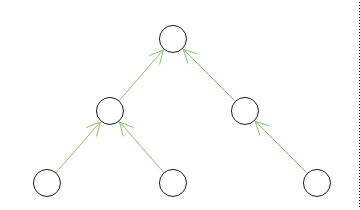
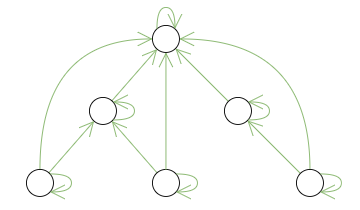
На следующих рисунках зеленым цветом условно обозначены данные, хранящиеся в реляционных таблицах, для рассмотренных способов представления иерархических структур.
| Список смежности | Подмножества |
|---|---|
 |
 |
| Вложенные множества | Материализованные пути |
|---|---|
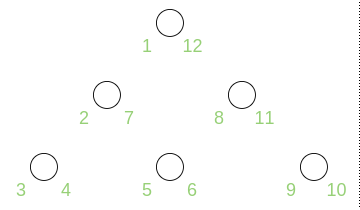 |
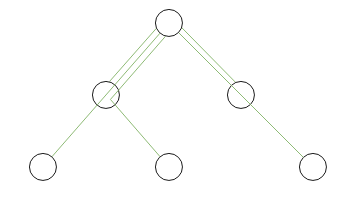 |
Для списка смежности и материализованных путей хранимая структура соответствует изначальной структуре в предметной области. Для подмножеств структура усложняется наличием рефлексивных и транзитивных связей между потомками и предками. В случае вложенных множеств хранимые значения имеют весьма опосредованное отношение к изначальной структуре.
| Список смежности | Подмножества | Вложенные множества | Материализованные пути | |
|---|---|---|---|---|
| Влияние размера дерева на скорость поиска поддеревьев | сильное: каждый новый уровень вложенности - это +1 SELECT | слабое | слабое, можно добавить индексы на left_key и right_key |
сильное (поиск по подстроке). Использование модуля ltree может ускорить операции так как поддерживает несколько типов индексов (B-дерево и GiST по значениям ltree) |
| Вставка узла | простая: не требует изменения других записей | сложная: вставка нового узла в обе таблицы + добавление записей для каждого дочернего узла | сложная: обновление всех узлов “правее и ниже” | сложная: обновление всех дочерних узлов |
| Перемещение узла | простое: не требует изменения других записей | сложная: обновление записей для предков и потомков узла | сложная: обновление всех узлов “правее и ниже” | сложная: обновление дочерних узлов и предков |
| Удаление узла | простое, каскадное | простое, каскадное | простое | сложное, поиск по подстроке |
| Избыточность хранения | нет | да | да | да |
| Поддержка целостности данных кроме ссылочной | не нужна | нужна | нужна | нужна |